Center point as Interest point.

Today I came up with an idea about "interest point". Briefly it is that "we can use not only corner points as interest point but also center points of circle".

I was using the Voodoo Camera Tracker.
Let me explain how it works briefly.

It first finds "corner points" from each image of a movie file.
And it figures out which corner point on the prior image is correspond to the point on the next image.
Finally it reconstructs the 3D coordinate position of the camera.

Here is the example. The first image is with the detected corner points. A green cross line indicates a corner.
The second image shows yellow lines which represent the corner point is traced from the prior image to the next image.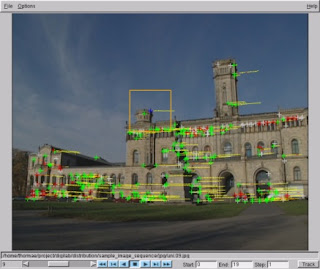
A problem that I found by using the Voodoo is that most of objects we are familiar in our life are round shape. And detecting corner doesn't give the enough information.

Thus I came up with the idea detecting and tracing the center of circle. We can find the center of a circle by this steps:
1. calculate the edges.
2. pick a point on the edges.
3. calculate the tangential line on the point.
4. find a perpendicular line from the tangential line.
5. pick an adjacent point of the point.
6. calculate a perpendicular line of the tangential line for the point.
7. find out the intersection of those perpendicular lines; this intersection will is a center of the circle or a part of circle.
7-a. if the intersecting point is too far from those points, those points doesn't share a same center.
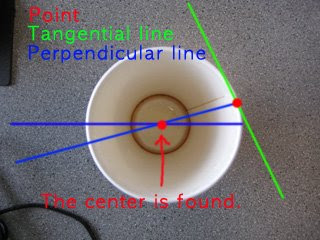As you can see above, this way doesn't require a complete circle. A part of arc is sufficient.

We can repeatedly calculate this process and we can segment arcs that consist of those points that shares a identical center. Here the segmenting is not the purpose but we can drop some of too short arcs from our further calculations by segmenting arcs.

A problem raises when we consider the fact that a circle shape can become a ellipse shape when the camera moves. See the image below. The position of the camera moved to down and the shape became ellipse from circle. In order to use the center point as interest point the position of the center point must be stable.


Here the question is how to find the center of the ellipse.
The formula of the ellipse is here:
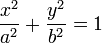We want to find the center of the ellipse, so that we need to add the variable for the center like this: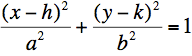where (h,k) is the center of the ellipse.

The formula now consists of x, y variables and 4 constants. We want to find out the constants: a, b, h, and k. We pick 4 sample points which are all adjacent from the edge image. And we can calculate the center: h, and k.
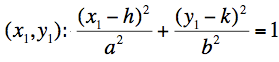
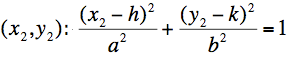
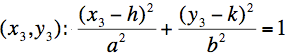
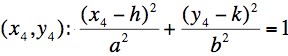x1, x2, x3, x4, y1, y2, y3 and y4 are all actual numbers from the edge images so that we can solve these 4 formula and get the center of the ellipse.

This way gives a stable center point of circles, arcs, and ellipses, regardless the angle from the camera. Finally we can use the stable center points as interest points.