HeteroVector for software testing.

I spend almost 3 days making this simple package, HeteroVector.

HeteroVector is a kind of std::vector. A difference is that HeteroVector can contain different types as 2 dimensional array. Let me give you an simple test case here:

int arg1[ ] = { 1, 2 };
char arg2[ ] = "amz";
float arg3[ ] = { 1.1f, 2.2f };

typedef LOKI_TYPELIST_3(int, char, float) MyInputTypes; // from Loki library

HeteroVector< MyInputTypes > values;
values.set< 0 >( arg1 );
values.set< 1 >( arg2 );
values.set< 2 >( arg3 );

ASSERT_EQ(1, values.get< 0 >( 0 ));
ASSERT_EQ(2, values.get< 0 >( 1 ));
ASSERT_EQ('a', values.get< 1 >( 0 ));
ASSERT_EQ('m', values.get< 1 >( 1 ));
ASSERT_EQ('z', values.get< 1 >( 2 ));
ASSERT_EQ(1.1f, values.get< 2 >( 0 ));
ASSERT_EQ(2.2f, values.get< 2 >( 1 ));

Here the object "values" represent this 2 dimensional array.
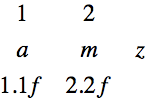Note that it contains three different types. Each row can contain different type but each columns in a same row must be the same type. The type is forced by compiler so that nobody can make mistake; it was possible because I was using template meta programming.

You may noticed that the way to access each value is not usual. For example, the code accessing the value 1 is "values.set < 0 > ( 0 );" The first value, which is for "row", is not method argument, but template argument so that it is "<" and ">". The second value is the method argument. The value for the template argument is technically type indicator, which is "int, char, float" in this case.

Let's go one more step. A testing code for "Factorial" is below:

int factorial(int nThStep) {
if(nThStep == 0) return 1;
return factorial(nThStep -1) * nThStep;
}

TEST(HeteroVector, Factorial) {
// This example shows how input and output values can be paired.
typedef LOKI_TYPELIST_2(int, int) FactorialTypes;
const unsigned int input = 0;
const unsigned int output = 1;

HeteroVector< FactorialTypes > inputs_outputs;
int inputs[] = { 0, 1, 2, 3, 4 };
int outputs[]= { 1, 1, 2, 6, 23 };
inputs_outputs.set< input >( inputs );
inputs_outputs.set< output >( outputs );
inputs_outputs.replace< output >( 4, 24 );

for(unsigned int nTh = 0; nTh < inputs_outputs.size< input >>(); ++nTh)
ASSERT_EQ(inputs_outputs.get< output >(nTh),
factorial( inputs_outputs.get< input >(nTh) ) );
}

The data for testing is all managed by the HeteroVector. The variable "inputs_outputs" represent this 2 dimensional array:
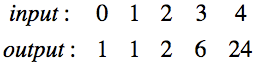Note that the values for the template arguments can be replaced by meaningful name. In next example, I will show you that we can also use "enum".

Here you may think we don't need to use HeteroVector for this factorial function testing. We can also replace it with two vectors, which will be "vector inputs", and "vector outputs". But it is just an example that I want to show how to use.

Let me give you an example for testing Switch function.

bool switchOnOff( bool switch1, bool switch2, bool switch3 ) {
return switch1 && (switch2 || switch3);
}

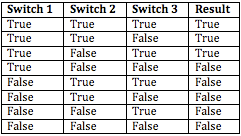The function, switchOnOff, requires three boolean arguments. Therefore we need to test 8 cases ( = 2 * 2 * 2 ). I drawn a table here:My additional implementation for HeteroVector generate those Combination of three "true/false" values. The testing code is here:

TEST(CoverageTest, AllCombinationsCoverage) {
typedef LOKI_TYPELIST_3(bool, bool, bool) Booleans;
enum { switch1, switch2, switch3 };
HeteroVector< Booleans > inputs;

bool true_false[] = { true, false };
bool true_only[] = { true };

inputs.set< switch1 >( true_false );
inputs.set< switch2 >( true_only );
inputs.set< switch3 >( true_false );
const bool expected[] = {
/*TTT*/ true,
/*FTT*/ false,
/*TTF*/ true,
/*FTF*/ false };

HeteroVector< Booleans > ACoC = allCombinationsCoverage(inputs);
ASSERT_EQ(sizeof(expected)/sizeof(bool), ACoC.size< switch1 >());
ASSERT_TRUE( ACoC.size< switch1 >() == ACoC.size< switch2 >() );
ASSERT_TRUE( ACoC.size< switch2 >() == ACoC.size< switch3 >() );

for(unsigned int idx = 0; idx < ACoC.size< switch1 >(); ++idx)
ASSERT_EQ( expected[idx],
switchOnOff(
ACoC.get< switch1 >(idx),
ACoC.get< switch2 >(idx),
ACoC.get< switch3 >(idx)
) ) < < idx; }

This code is a little bit different from the table, because I fixed the second argument in a value, "true," in order to show that we don't always need to generate for every possible cases but we can select some input values for our interest. By the constrain the code generate only 4 cases ( 2 * 1 * 2), but we can, of course, generate 8 cases easily.

Note that the template argument is replaced by ENUM values, which makes easier to read.

I have also implemented Base Choice Coverage, which is introduced in my professors book, "Introduction to Software Testing" (written by Paul Ammann and Jeff Offutt)

The basic idea of Base Choice Coverage is that we choose a default set of input values and change only one value from it rather than using all combination. Therefore the input set of BCC will be like this table:
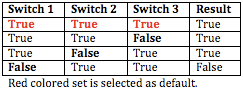The testing case will give you how to use my implementation for BCC:

TEST(CoverageTest, BaseChoicesCoverage) {
typedef LOKI_TYPELIST_3(bool, bool, bool) Booleans;
enum { switch1, switch2, switch3 };
HeteroVector< Booleans > inputs;

bool true_false[] = { true, false };
bool false_only[] = { false };

inputs.set< switch1 >( true_false );
inputs.set< switch2 >( true_false );
inputs.set< switch3 >( false_only );
const bool expected[] = {
/*TTF*/ true,
/*FTF*/ false,
/*TFF*/ false };

HeteroVector< Booleans > BCC = baseChoiceCoverage(inputs);
ASSERT_EQ(sizeof(expected)/sizeof(bool), BCC.size< switch1 >());
ASSERT_TRUE( BCC.size< switch1 >() == BCC.size< switch2 >() );
ASSERT_TRUE( BCC.size< switch2 >() == BCC.size< switch3 >() );

for(unsigned int idx = 0; idx < BCC.size< switch1 >(); ++idx)
ASSERT_EQ( expected[idx],
switchOnOff(
BCC.get< switch1 >(idx),
BCC.get< switch2 >(idx),
BCC.get< switch3 >(idx)
) ) < < idx; }

The code is, again, different from the table that I showed above. The testing code fixed 3rd value at "false". Therefore it generates only 3 cases but it is, again, easy to generate 4 cases, which satisfies BCC correctly. I just wanted to show the implementation has flexability for choice.

I spent 3 days implementing this code. It was very hard because I used template meta programming which gives programmers desperate. In other word, my implementation strongly check Type. Compiler will forece users not to make mistake at compile time not at run-time. And it also increases run-time speed, because many parts of calculation will be done at compile time.

I like to share my effort with everybody. Any comments are welcome. You can download the source code here: HeteroVector.

I used Loki library, which is famous meta programming library. It is open source so that anybody can download; in fact my implementation requires Loki library. You can find the most recent version of Loki here.

Using interface in C++

Yesterday I found that this article has some problem:
http://www.codeguru.com/cpp/cpp/cpp_mfc/oop/article.php/c9989

By its nature interface brings multi-inheritance and it can cause "diamond problem".

In order to solve this problem you have to make sure the "implements" always use "public virtual" rather than just "public". See virtual inheritance.

My implementation is here:

#define IMPLEMENTS( INTERFACE_CLASS_NAME ) public virtual INTERFACE_CLASS_NAME

#define EXTENDS_INTERFACE( INTERFACE_CLASS_NAME ) public virtual INTERFACE_CLASS_NAME

The virtual destructor problem is less important because compiler will notice the programmer when a class has some virtual method without a virtual destructor.

Jumble and muJava

I'm reading a book, "Test-Driven Development, Kent Beck, 2003". And the book briefly mentioned "defect insertion, page86". Thus I curiously checked the software, "Jester" and I found it was (surprisingly) Mutation testing tool, which my professor, Jeff Offutt is strong at.

However, the software, Jester, seems not to be maintained anymore. I found another interesting software, "Jumble". The usage was very easy and simple. BUT a big shortcoming is that it doesn't support as many mutation operations as muJava does.Unfortunately, muJava, which is developed by Jeff Offutt, doesn't support JUnit while Jumble does. Somebody need to make muJava work with JUnit sooner or later. Or we need to make Jumble support other operations.

I recommend you use Jumble rather than muJava due to the supporting JUnit; it is better than not using. But we still don't have any free mutation testing tool for C++, although there are some commercial.

Center point as Interest point.

Today I came up with an idea about "interest point". Briefly it is that "we can use not only corner points as interest point but also center points of circle".

I was using the Voodoo Camera Tracker.
Let me explain how it works briefly.

It first finds "corner points" from each image of a movie file.
And it figures out which corner point on the prior image is correspond to the point on the next image.
Finally it reconstructs the 3D coordinate position of the camera.

Here is the example. The first image is with the detected corner points. A green cross line indicates a corner.
The second image shows yellow lines which represent the corner point is traced from the prior image to the next image.
A problem that I found by using the Voodoo is that most of objects we are familiar in our life are round shape. And detecting corner doesn't give the enough information.

Thus I came up with the idea detecting and tracing the center of circle. We can find the center of a circle by this steps:
1. calculate the edges.
2. pick a point on the edges.
3. calculate the tangential line on the point.
4. find a perpendicular line from the tangential line.
5. pick an adjacent point of the point.
6. calculate a perpendicular line of the tangential line for the point.
7. find out the intersection of those perpendicular lines; this intersection will is a center of the circle or a part of circle.
7-a. if the intersecting point is too far from those points, those points doesn't share a same center.
As you can see above, this way doesn't require a complete circle. A part of arc is sufficient.

We can repeatedly calculate this process and we can segment arcs that consist of those points that shares a identical center. Here the segmenting is not the purpose but we can drop some of too short arcs from our further calculations by segmenting arcs.

A problem raises when we consider the fact that a circle shape can become a ellipse shape when the camera moves. See the image below. The position of the camera moved to down and the shape became ellipse from circle. In order to use the center point as interest point the position of the center point must be stable.


Here the question is how to find the center of the ellipse.
The formula of the ellipse is here:
We want to find the center of the ellipse, so that we need to add the variable for the center like this:where (h,k) is the center of the ellipse.

The formula now consists of x, y variables and 4 constants. We want to find out the constants: a, b, h, and k. We pick 4 sample points which are all adjacent from the edge image. And we can calculate the center: h, and k.
x1, x2, x3, x4, y1, y2, y3 and y4 are all actual numbers from the edge images so that we can solve these 4 formula and get the center of the ellipse.

This way gives a stable center point of circles, arcs, and ellipses, regardless the angle from the camera. Finally we can use the stable center points as interest points.

My project is going on..

Today I spend a whole day figuring out how to use Voodoo Camera Track. It was supposed to be easy to use, but I found that it is very sensitive for the contents of the movie clip. I tried several different objects and different options in Voodoo Camera Track. It turned out that the vehicle movie clips are easiest objects for Voodoo.

Thus I decided to use the movie clip of my car; BB helped me to take it. The movie clip comprise about 400 frames and I took the sequential image files with VirtualDub. VirtualDub had very simple and nice exporting functionality; I also want to mention that I spent several hours to find a software to get the sequential images from a movie file. On the movie clip, the camera moves around the car clock-wise.
Finally VooDoo Camera Tracker gave me the position data of the camera. The visualized figure in 3D coordinate is below:The green lines represent the direction of down side of the camera, the blue lines indicate the direction that the camera is directing at each point. I believe the red lines represent the position of the camera. The white dots are called interest clouds. Each white dot indicates a corner point of images in 3D coordinate.

How to get optimized code in Agile process.

These days I'm fascinated by the idea of Agile process. I have read the 500 page book, "Agile software development" 2002, in 4 days, and I borrowed several more books about agile and eXtreme Programming.
This morning when I was reading a book, "Clean Code", I was thinking what if clients want my program to be faster. The book mainly focuses on Maintainability and Readability of source code rather than Optimization. Generally optimization harms maintainability and increases complexity.

However the performance is very important for game programming, so that optimization is inevitable.
The book, "Clean Code", said, "Make your program work first and then make it right." I want to add here: "Make it work, make it right and make it fast".

How do we make a program work? It assumes that we uses "Test cases first", and we can make a program working for the test cases. And then we need to clean the code, making right for short.

What I want to suggest here is once we got the right code, we keep the right code as the "base code" and we build "Temporary Fast Codes". Since we have the right code, the behavior of the right code and the fast code must be identical. Thus we can use the right code as an automatic test case generator, for example:

GameComponent rightCode = new RightImpl();
GameComponent fastCode = new FastImpl();
for ( int i = 0; i < 1000; ++i )
assertEquals( rightCode.do(i), fastCode.do(i) );

The point is that we don't expect we can maintain the optimized fast code. It should be treated as "Temporary Code". When the requirements change, the right code will grow up while the temporary code doesn't. We throw the fast code away and we will use the right code until we get the temporary fast code again.

Following this idea, we keep the basic principle of Agile process and we can also get the optimized (temporary) code. In game development process, we may develop the optimized code only at the last phase of the process, so that we can focus solely on right code during most of iterations without worrying about optimization.